OSB-skivan har en tjocklek av 25 mm och är orienterad med sin huvudspånriktning parallellt med limträbalkarna i detta exempel. Livet har dimensionerna 42×315 mm samt en underfläns med dimensionerna 225×42 mm. Balkarna placeras med centrumavstånd 0,6 m.
Bjälklagssystemet kan antas uppvisa full samverkan. Bjälklaget har en längd av 5,5 m (i livens riktning) och en bredd av 8,0 m. Bjälklaget är fritt upplagt.
Massan av bjälklaget är 45 kg/m2.
Utför en dimensioneringskontroll för att bekräfta att bjälklagets vibrationsbeteende kommer att vara acceptabelt, se Dimensionering av träkonstruktioner Del 2: Avsnitt 9.4 eller Eurokod 5: Avsnitt 7.3.
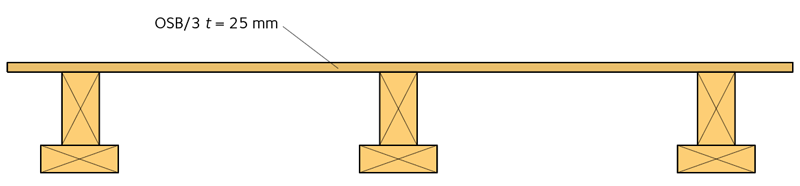
Bild 1.
Transformera först tvärsnittet till ett fiktivt tvärsnitt bestående av limträ, GL28cs.
OSB-skivans effektiva bredd beff kan sättas till 0,15ℓ enligt Dimensionering av träkonstruktioner Del 1: Tabell 5.1 eller Eurokod 5: Tabell 9.1. Då ℓ = 5,5 m, blir beff = 0,825 m, vilket är större än 0,6 m. Detta innebär att hela bredden av OSB-flänsen kan utnyttjas i beräkningen av tröghetsmomentet I.
Elasticitetsmodul för GL28cs: E0,mean = 12 500 MPa
Elasticitetsmodul för OSB: Em = 4 930 MPa
Den fiktiva bredden för flänsen erhålls ur:
\(\displaystyle {b_{{\rm f_u},\rm fic}} = \frac{{{E_\rm m}}}{{{E_{\rm 0,mean}}}}{b_\rm u} = \frac{{4930}}{{12500}} \cdot 600 = 237\,{\rm{ mm}}\)
Tvärsnittsarean:
\(\displaystyle {A_\rm c} = b{}_{{\rm f_l}} \cdot {h_\ell } + b_\rm w \cdot {h_\rm w} + b_{\rm fu,fic} \cdot {h_\rm u} = 225 \cdot 42 + 42 \cdot 315 + 237 \cdot 25 = 28596\,{\rm{ m}}{{\rm{m}}^{\rm{2}}}\)
Tyngdpunkten (från den undre kanten):
\( \begin{array}{l}\displaystyle {x_{\rm tp}} = \frac{{b{}_{{\rm f_l}} \cdot {h_\ell } \cdot \frac{{{h_\ell }}}{2} + b_\rm w \cdot {h_\rm w} \cdot \left( {{h_\ell } + \frac{{{h_\rm w}}}{2}} \right) + b_{\rm fu,fic} \cdot {h_\rm u} \cdot \left( {{h_\ell } + {h_\rm w} + \frac{{{h_\rm u}}}{2}} \right)}}{{{A_c}}} = \\ \displaystyle \frac{{225 \cdot 42 \cdot \frac{{42}}{2} + 42 \cdot 315 \cdot \left( {42 + \frac{{315}}{2}} \right) + 237 \cdot 25 \cdot \left( {42 + 315 + \frac{{25}}{2}} \right)}}{{28596}} = 176\,{\rm{ mm}} \end{array}\)
Tröghetsmomentet för undre flänsen:
\( \begin{array}{l}\displaystyle {I_{{\rm f_l}}} = \frac{{{b_{{\rm f_l}}}{h_\ell }^3}}{{12}} + {b_{{\rm f_l}}}{h_\ell } \cdot {\left[ {{x_{\rm tp}} - \left( {\frac{{{h_{{\rm f_l}}}}}{2}} \right)} \right]^2} = \\ \displaystyle \frac{{0,225 \cdot {{0,042}^3}}}{{12}} + 0,225 \cdot 0,042 \cdot {\left[ {0,176 - \left( {\frac{{0,042}}{2}} \right)} \right]^2} = 227 \cdot {10^{ - 6}}\,{\rm{ }}{{\rm{m}}^{\rm{4}}} \end{array}\)
Tröghetsmomentet för övre flänsen:
\( \begin{array}{l}\displaystyle {I_{{f_\rm u}}} = \frac{{{b_{{\rm f_u}}}{h_\rm u}^3}}{{12}} + {b_{{\rm f_u}}}{h_\rm u} \cdot {\left[ {{x_{\rm tp}} - \left( {{h_{{\rm f_l}}} + {h_\rm w} + \frac{{{h_{{\rm f_u}}}}}{2}} \right)} \right]^2} = \\ \displaystyle \frac{{0,237 \cdot {{0,025}^3}}}{{12}} + 0,237 \cdot 0,025 \cdot {\left[ {0,176 - \left( {0,042 + 0,315 + \frac{{0,025}}{2}} \right)} \right]^2} = 222 \cdot {10^{ - 6}}\,{\rm{ }}{{\rm{m}}^{\rm{4}}} \end{array}\)
Tröghetsmomentet för livet:
\( \begin{array}{l}\displaystyle {I_\rm w} = \frac{{{b_\rm w}{h_\rm w}^3}}{{12}} + {b_\rm w}{h_\rm w} \cdot {\left[ {{x_{\rm tp}} - \left( {{h_{{\rm f_l}}} + \frac{{{h_\rm w}}}{2}} \right)} \right]^2} = \\ \displaystyle \frac{{0,042 \cdot {{0,315}^3}}}{{12}} + 0,042 \cdot 0,315 \cdot {\left[ { - 0,176 + 0,042 + \frac{{0,315}}{2}} \right]^2} = 117 \cdot {10^{ - 6}}\,{\rm{ }}{{\rm{m}}^{\rm{4}}} \end{array}\)
Tröghetsmomentet:
\(\displaystyle I = I_{{\rm f_l}} + I_{{\rm f_u}} + {I_\rm w} = 227 \cdot {10^{ - 6}} + 222 \cdot {10^{ - 6}} + 117 \cdot {10^{ - 6}} = 566 \cdot {10^{ - 6}}\,{\rm{ }}{{\rm{m}}^4}\)
Tröghetsmomentet för golvbeläggningen/meter bredd:
\(\displaystyle {I_\rm f} = \frac{{{b_\rm t}{h_{{\rm f_u}}}^3}}{{12}} = \frac{{1 \cdot {{0,025}^3}}}{{12}} = {\rm{1,3}} \cdot {\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}}{\rm{ }}\,{{\rm{m}}^{\rm{4}}}\)
Bjälklagsstommens bredd, B = 8 m
Massan av bjälklaget (kg/m2), m = 45 kg/m2
a. Kontrollera bjälklagets lägsta egenfrekvens:
\(\displaystyle {f_1} = \frac{\pi }{{2{\ell ^2}}}\sqrt {\frac{{{{\left( {EI} \right)}_\ell }}}{m}} \)
\(\displaystyle {f_1} = \frac{\pi }{{2 \cdot {{5,5}^2}}}\sqrt {\frac{{{{\left(\displaystyle {\frac{{12500 \cdot 10{}^6 \cdot 566 \cdot {{10}^{ - 6}}}}{{0,6}}} \right)}_{}}}}{{45}}} = 26,6\)
Den lägsta egenfrekvensen för bjälklaget är acceptabel, då den är högre än 8 Hz och ekvationerna som återfinns i Dimensionering av träkonstruktioner Del 1: Avsnitt 7.3.3.1 kan användas för en vibrationskontroll.
b. Kontrollera bjälklagets statiska nedböjning:
Största tillåtna nedböjning är a = 1,5 mm, för en punktlast av 1 kN.
\(\displaystyle w = \frac{{P{{\ell }^3}}}{{48EI}}\)
Kontrollera en enskild balk:
P = 1 000 N
\(\displaystyle w = \frac{{1000 \cdot {{5,5}^3}}}{{48 \cdot 12,5 \cdot {{10}^9} \cdot 566 \cdot {{10}^{ - 6}}}}\,\; \cdot \;1000 = 0,5\,{\rm{ mm}}\)
Bjälklagets nedböjning är mindre än det tillåtna värdet.
Det följande bör också gälla:
\(\displaystyle v \le {b^{\left( {{f_1}\zeta - 1} \right)}}\)
där v är hastighetsresponsen på enhetsimpuls (m / (Ns2). ζ är den relativa dämpningen, vilken normalt kan sättas till 0,01. Konstanten b för kontroll av hastighetsresponsen på enhetsimpuls kan sättas till 100 (se Dimensionering av träkonstruktioner Del 2: Avsnitt 9.4):
\(\displaystyle v \le {b^{\left( {{f_1}\zeta - 1} \right)}} = {100^{\left( {26,6 \cdot 0,01 - 1} \right)}} = 0,034\)
Hastighetsresponsen på enhetsimpuls erhålls genom:
\(\displaystyle v = \frac{{4\left( {0,4 + 0,6{n_{40}}} \right)}}{{mB{\ell } + 200}}\)
där n40 är antalet moder av första ordningen, med egenfrekvenser upp till 40 Hz och B är bjälklagsbredden. Värdet av n40 kan beräknas ur:
\(\displaystyle {n_{40}} = {\left\{ {\left( {{{\left( {\frac{{40}}{{{f_1}}}} \right)}^2} - 1} \right){{\left( {\frac{B}{{\ell }}} \right)}^4}\frac{{\left( {EI} \right){}_\ell }}{{{{\left( {EI} \right)}_{\mathop{\rm B}\nolimits} }}}} \right\}^{0,25}}\)
\(\displaystyle {n_{40}} = {\left\{ {\left( {{{\left( {\frac{{40}}{{26,6}}} \right)}^2} - 1} \right){{\left( {\frac{{8000}}{{5500}}} \right)}^4}\frac{{\left( {\frac{{12500 \cdot 566}}{{0,6}}} \right)}}{{\left( {4930 \cdot 1,3} \right)}}} \right\}^{0,25}} = 10,1\)
Hastighetsresponsen på enhetsimpuls blir då:
\(\displaystyle v = \frac{{4\left( {0,4 + 0,6 \cdot 10,1} \right)}}{{45 \cdot 8 \cdot 5,5 + 200}} = 0,012\)
Då hastighetsresponsen på enhetsimpuls för bjälklaget är lägre än det tillåtna värdet, är det acceptabelt. Bjälklaget uppfyller vibrationskraven i Eurokod 5.

