4.5.4 Dimensionering av spikningsplåtar i KL-trä

Laskar med varierande hålmönster, tjocklek och ytbehandling kan beställas av tillverkare som levererar stansade infästningar. Priset är oftast lägst om hålen stansas, vilket betyder att plåttjockleken inte får överskrida håldiametern. Hålen bör vara ungefär 1 mm större än fästdonets ytterdiameter.

Innovativa förbandslösningar, här i form av X-RAD.

Kontroll och dimensionering av stålplåtar
Den här typen av förband överför tryckande vertikalkraft med hjälp av kontakt mellan KL-träskivan och grunden. Den horisontella kraften F_E,y och den eventuella vertikala dragkraften F_E,x överförs av spikarna till stålplåten, som för dem vidare till grunden, se figur 4.32. För ingjutna plåtar eller för plåtar som är svetsade mot ingjutna svetsplåtar, betraktas oftast plåten som en fast inspänd konsol i grunden.

Följande brottmoder bör kontrolleras:

• skjuvning av spikinfästningen i KL-trä
• klossbrott, se Eurokod 5, bilaga A
• brott i stålplåten förorsakat av moment, normalkraft och tvärkraft (både bruttotvärsnitt och nettotvärsnitt)
• knäckning av stålplåt förorsakad av normalkraft.

Vid kontroll av skjuvning av spikinfästningen antas horisontalkraften och den eventuella vertikala dragkraften verka i spikgruppens tyngdpunkt. Den resulterande kraften F_E blir då enligt ekvation 4.9:

4.9  \({F_{\rm{E}}} = \sqrt {F_{{\rm{E}},{\rm{x}}}^2 + F_{{\rm{E}},{\rm{y}}}^2} \)

För att bestämma antalet spikar hämtas värden för bärförmågan per fästdon, F_v,Rd enligt Eurokod 5 eller verifierade värden från tillverkare. För spikar med diameter mindre än 8 mm är bärförmågan densamma oberoende av kraftens riktning. Antalet spikar, n, kan då bestämmas enligt ekvation 4.10:

4.10  \(n = \frac{{{F_{\rm{E}}}}}{{{F_{{\rm{v}},{\rm{Rd}}}}}}\)

Om spikarnas centrumavstånd i fiberriktningen sätts till minst 14d behöver man inte begränsa det effektiva antalet spikar i en rad, se Eurokod 5, tabell 8.1. Om standardiserade spikningsplåtar används bestäms avståndet också av plåtens hålmönster.

Klossbrott i förband kan lämpligen kontrolleras enligt Eurokod 5, bilaga A. Om stålplåten belastas med en vertikal och en horisontell kraft, ger horisontalkraftens excentricitet upphov till ett böjmoment. I stålplåtens fast inspända tvärsnitt blir momentet:

4.11  \({M_{\rm{E}}} = {F_{{\rm{E}},{\mathop{\rm y}\nolimits} }} \cdot {e_1}\)

I hålraden med största påkänningen gäller:

4.12  \({M_{\rm{E}}} = {F_{{\rm{E}},{\mathop{\rm y}\nolimits} }} \cdot {e_2}\)

Spänningarna i stålplåtens olika snitt beräknas utgående från momentet och de vertikala och horisontella krafterna. Om stålplåten är tunn, kan det vara nödvändigt att kontrollera risken för knäckning av plåten. Om fästdonens avstånd i stålplåten utförs enligt rekommendationer behöver detta inte kontrolleras. Därför bör avståndet mellan hålen i lasken och dessutom mellan den första hålraden och grunden inte vara större än det minsta av 14t (t är plåttjockleken) eller 200 mm. Infästningen av lasken i grunden ska också kontrolleras.

Kontroll av stålplåtar
Kontroll av stålplåtar görs enligt Eurokod 3 – Dimensionering av stålkonstruktioner. Olika brott kan uppträda i stålplåten, drag-, tryck-, skjuv- och böjbrott, en kombination av dessa samt hålkantbrott men där hålkantbrott med normalt använda dimensioner är ovanligt.

För dragbrott i stålplåt kontrolleras hela tvärsnittet och nettotvärsnittet (del av tvärsnittet som återstår när hålen för fästdonen beaktas). Bärförmågan N_pl,Rd för hela tvärsnittet kan beräknas enligt ekvation 4.13:

4.13  \({N_{{\rm{pl}},{\rm{Rd}}}} = \frac{{{f_{\rm{y}}} \cdot A}}{{{\gamma _{{\rm{M}}0}}}}\)

Bärförmågan N_u,Rd för nettotvärsnittet är:

4.14  \({N_{{\rm{u}},{\rm{Rd}}}} = \frac{{0,9 \cdot {f_\rm u} \cdot {A_{{\rm{net}}}}}}{{{\gamma _{{\rm{M}}2}}}}\)

4.15  \({\gamma _{{\rm{M}}2}} = {\rm max}\left[ {1,1;\;0,9 \cdot \frac{{{f_{\rm{u}}}}}{{{f_{\rm{y}}}}}} \right]\)

där:

fy	är sträckgränsen för stålmaterialet.
fu	är brottgränsen för stålmaterialet.
A	är tvärsnittets bruttoarea för stålplåten.
Anet	är tvärsnittets nettoarea för stålplåten (genom en hålrad).
γM0	är partialkoefficienten för materialet, 1,0.

 

 

 

Tryckbrott i stålplåten kontrolleras och bärförmågan vid tryck N_c,Rd beräknas enligt ekvation 4.16:

4.16  \({N_{{\rm{c}},{\rm{Rd}}}} = \frac{{{f_{\rm{y}}} \cdot A}}{{{\gamma _{{\rm{M}}0}}}}\)

där:

fy	är sträckgränsen för stålmaterialet.
A	är tvärsnittets bruttoarea för stålplåten.
γM0	är partialkoefficienten för materialet, 1,0.

 

 

Kontroll av buckling av stålplåten behöver inte göras om avståndet mellan fästdonen är mindre än a₁ och där a₁ kan skrivas som:

4.17  \({{\mathop{\rm a}\nolimits} _1} \le 9t \cdot \varepsilon = 9t\sqrt {\frac{{235}}{{{f_{\rm{y}}}}}} \)

där:

fy	är sträckgränsen för stålmaterialet.
t	är stålplåtens tjocklek.
ε	är en dimensionslös faktor för bestämning av stålplåtens tvärsnittsklass.

 

 

Om avståndet mellan fästdonen är större än a₁ kontrolleras plåten genom att plåten betraktas som en tryckt pelare med knäcklängden 0,6a₁.

Böjbrott i stålplåten kontrolleras och bärförmågan M_c,Rd vid böjning då tvärsnittet blir fullständigt plastiskt beräknas enligt ekvation 4.18, för moment kring en tyngdpunktsaxel för ett tvärsnitt:

4.18  \({M_{{\rm{c}},{\rm{Rd}}}} = \frac{{{W_{{\rm{pl}}}} \cdot {f_{\rm{y}}}}}{{{\gamma _{{\rm{M}}0}}}}\)

där:

Wpl	är det plastiska böjmotståndet för stålplåten.
fy	är sträckgränsen för stålmaterialet.
γM0	är partialkoefficienten för materialet, 1,0.

 

 

För ett rektangulärt tvärsnitt fås:

4.19  \({W_{{\rm{pl}}}} = \frac{{b \cdot {h^2}}}{4}\)

där:

h	är tvärsnittets höjd.
b	är tvärsnittets bredd.

 

 

Hålens inverkan i den tryckta zonen behöver inte beaktas om hålen är fyllda med fästdon. I den dragna zonen behöver inte hålen beaktas så länge följande uppfylls:

4.20  \(\frac{{{A_{{\rm{net}}}} \cdot 0,9 \cdot {f_{\rm{u}}}}}{{{\gamma _{{\rm{M}}2}}}} \ge \frac{{A \cdot {f_{\rm{y}}}}}{{{\gamma _{{\rm{M}}0}}}}\)

4.21  \({\gamma _{{\rm{M}}2}} = {\rm{max}}\left[ {1,1;\;0,9 \cdot \frac{{{f_{\rm{u}}}}}{{{f_{\rm{y}}}}}} \right]\)

där:

fy	är sträckgränsen för stålmaterialet.
fu	är brottgränsen för stålmaterialet.
A	är tvärsnittets bruttoarea för stålplåten.
Anet	är tvärsnittets nettoarea för stålplåten (genom en hålrad).
γM0	är partialkoefficienten för materialet, 1,0.

 

 

 

Skjuvbrott i stålplåten kontrolleras och tvärkraftsbärförmågan V_c,Rd beräknas enligt ekvation 4.22 om hela tvärsnittet blir fullständigt plastiskt:

4.22  \({V_{{\rm{c}},{\rm{Rd}}}} = {V_{{\rm{pl}},{\rm{Rd}}}} = \frac{{{A_{\rm{v}}}\left( {{f_{\rm{y}}}/\sqrt 3 } \right)}}{{{\gamma _{{\rm{M}}0}}}}\)

där:

fy	är sträckgränsen för stålmaterialet.
Av	är tvärsnittets skjuvarea för stålplåten.
γM0	är partialkoefficienten för materialet, 1,0.

 

 

Brottkriterium enligt ekvation 4.23 kan användas när stålplåten utsätts för samtidigt verkande normalkrafter och tvärkrafter:

4.23  \({\left( {\frac{{{\sigma _{{\rm{x}},{\rm{Ed}}}}}}{{{f_{\rm{y}}}/{\gamma _{{\rm{M}}0}}}}} \right)^2} + {\left( {\frac{{{\sigma _{y,{\rm{Ed}}}}}}{{{f_{\rm{y}}}/{\gamma _{{\rm{M}}0}}}}} \right)^2} - \left( {\frac{{{\sigma _{{\rm{x}},{\rm{Ed}}}}}}{{{f_{\rm{y}}}/{\gamma _{{\rm{M}}0}}}}} \right)\left( {\frac{{{\sigma _{y,{\rm{Ed}}}}}}{{{f_{\rm{y}}}/{\gamma _{{\rm{M}}0}}}}} \right) + 3\left( {\frac{{{\tau _{{\rm{Ed}}}}}}{{{f_{\rm{y}}}/{\gamma _{{\rm{M}}0}}}}} \right) \le 1\)

där:

σx,Ed	är dimensioneringsvärdet för normalspänningen i stålplåtens längdriktning.
σy,Ed	är dimensioneringsvärdet för normalspänningen vinkelrätt mot stålplåtens längdriktning.
τEd	är dimensioneringsvärdet för skjuvspänningen.
fy	är sträckgränsen för stålmaterialet.
γM0	är partialkoefficienten för materialet, 1,0.

 

 

 

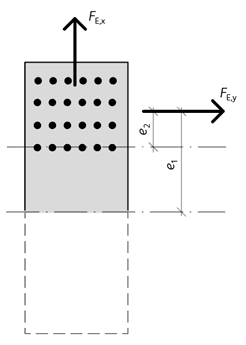
Figur 4.32 Infästning av KL-träväggskiva med laskar av stålplåt. Schematisk bild. Laskarna kan fästas med spikar eller träskruvar.