Normalkraften N, i ett godtyckligt tvärsnitt längs med bågen kan beräknas enligt följande:
11.1 \(N = H \cdot \cos \alpha + {V_\rm b} \cdot \sin \alpha \)
Tvärkraften V, i ett godtyckligt tvärsnitt längs med bågen, kan beräknas enligt följande:
11.2 \(V = - H \cdot \sin \alpha + {V_\rm b} \cdot \cos \alpha \)
där Vb är tvärkraften i en fritt upplagd balk med samma spännvidd och samma vertikallast som bågen i fråga och H är stödreaktionens horisontella komponent, se figur 11.7.
Det kritiska tvärsnittet befinner sig vanligtvis ungefär i spännviddens fjärdedelspunkt. Vid detta tvärsnitt kan vinkeln α beräknas enligt följande:
11.3a \(\alpha = \arcsin \left( {\frac{l}{{4 \cdot R}}} \right)\) för cirkelbågar
11.3b \(\alpha = \frac{{180}}{\pi } \cdot \arctan \left( {\frac{{2 \cdot f}}{l}} \right)\) för parabelbågar
Vid spännviddens fjärdedelspunkt kan höjden y0 för bågens systemlinje beräknas enligt följande:
11.4a \({y_0} = \frac{f}{2} - \frac{{{l^2}}}{{8 \cdot f}} + \sqrt {\frac{{{l^4}}}{{64 \cdot {f^2}}} + \frac{{{f^2}}}{4} + \frac{{{l^2}}}{{16}}}\) för cirkelbågar
11.4b \({y_0} = \frac{3}{4} \cdot f\) för parabelbågar
De kritiska lastkombinationerna som vanligtvis gäller vid dimensionering av treledsbågar är:
- Permanenta laster + jämnt fördelad snölast.
- Permanenta laster + triangulär snölast – olika stora på vardera båghalvan.
Resten av detta avsnitt ger anvisningar för beräkning av stödreaktioner och de inre krafterna (normalkrafter, tvärkrafter och böjmoment).
De följande anvisningarna gäller endast för cirkelformade bågar med förhållandet mellan pilhöjd och spännvidd f ⁄ l ≈ 0,15 och för parabelformade bågar som uppfyller följande ekvation:
11.5 \(y = \frac{{4 \cdot f}}{l} \cdot \left( {x - \frac{{{x^2}}}{l}} \right)\)
där x-axeln börjar vid bågens stöd och y är höjden för bågens systemlinje.
Permanenta laster + jämnt fördelad snölast
Vid belastning enligt figur 11.8, kan en treledsbåges stödreaktioner och inre krafter beräknas enligt följande:
Vertikal stödreaktion: (vid vänster stöd: Rl och vid höger stöd: Rr):
11.6 \({R_l} = {R_\rm r} = \frac{{\left( {{q_\rm r} + g} \right) \cdot l}}{2}\)
Horisontell stödreaktion:
11.7 \(H = \frac{{\left( {{q_\rm r} + g} \right) \cdot {l^2}}}{{8 \cdot f}}\)
Maximal normalkraft vid av spännvidden:
11.8 \(N = \frac{{\left( {{q_\rm r} + g} \right) \cdot {l^2}}}{{8 \cdot f}} \cdot \cos \alpha + \frac{{\left( {{q_\rm r} + g} \right) \cdot l}}{4} \cdot \sin \alpha \)
Böjmoment vid 1/4 av spännvidden:
11.9 \(M \approx 0\)
Tvärkraft vid stöd (x = 0):
11.10 \({V_{\rm sp}} = - \frac{{\left( {{q_\rm r} + g} \right) \cdot {l^2}}}{{8 \cdot f}} \cdot \sin {\alpha _{\rm spr}} + \frac{{\left( {{q_\rm r} + g} \right) \cdot l}}{2} \cdot \cos {\alpha _{\rm spr}}\)
Tvärkraften vid bågens nock är lika med noll.
Permanenta laster + triangulär snölast
Vid belastning enligt figur 11.9, kan en treledsbåges stödreaktioner och inre krafter beräknas enligt följande:
Vertikal stödreaktion, vid vänster stöd:
11.11 \({R_l} = \frac{7}{{32}} \cdot {q_\rm t} \cdot l + \frac{1}{2} \cdot g \cdot l\)
Vertikal stödreaktion, vid höger stöd:
11.12 \({R_\rm r} = \frac{5}{{32}} \cdot {q_\rm t} \cdot l + \frac{1}{2} \cdot g \cdot l\)
Horisontell stödreaktion:
11.13 \(H = \frac{3}{{64}}\frac{{\left( {{q_\rm t}} \right) \cdot {l^2}}}{f} + \frac{{\left( g \right) \cdot {l^2}}}{{8 \cdot f}}\)
Maximal normalkraft vid 1/4 av spännvidden:
11.14 \(N = \frac{{{l^2}}}{{8 \cdot f}} \cdot \left( {g + \frac{{3 \cdot {q_\rm t}}}{8}} \right) \cdot \cos \alpha + \frac{l}{4} \cdot \left( {g + \frac{{3 \cdot {q_\rm t}}}{8}} \right) \cdot \sin \alpha \)
Böjmoment vid 1/4 av spännvidden (y0 enligt ekvation 11.4):
11.15 \(M = \frac{{{q_\rm t} \cdot {l^2}}}{{22,6}} - \left( {\frac{3}{{64}}\frac{{\left( {{q_\rm t}} \right) \cdot {l^2}}}{f} + \frac{{\left( g \right) \cdot {l^2}}}{{8 \cdot f}}} \right) \cdot {y_0}\)
Tvärkraft vid stöd (x = 0):
11.16 \({V_{\rm spring}} = - \frac{{{l^2}}}{{8 \cdot f}} \cdot \left( {g + \frac{{3 \cdot {q_\rm t}}}{8}} \right) \cdot \sin {\alpha _{\rm spr}} + \frac{l}{2} \cdot \left( {g + \frac{{5 \cdot {q_\rm t}}}{{16}}} \right) \cdot \cos {\alpha _{\rm spr}}\)
Tvärkraft vid bågens nock:
11.17 \({V_{\rm ridge}} = \frac{{{q_\rm t} \cdot l}}{{32}}\)

Gislavedsbron
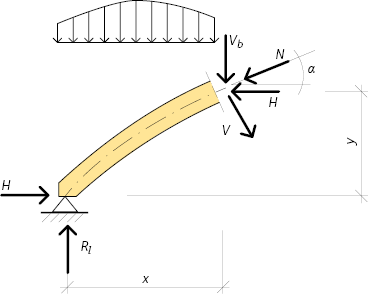
Figur 11.7 Inre krafter i ett godtyckligt tvärsnitt av bågen.
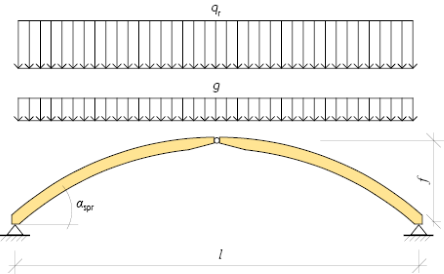
Figur 11.8 Treledsbåge belastad med permanent last och jämnt fördelad snölast.
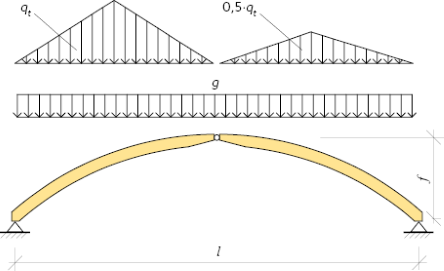
Figur 11.9 Treledsbåge belastad med permanent last och triangulär snölast enligt Eurokod 1-3.
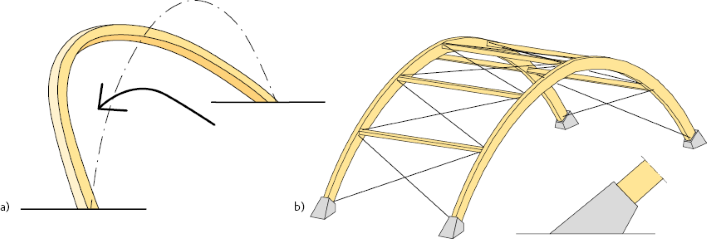
Figur 11.10 En båges beteende i sidled vid montage.
a) En båge kan tippa i sidled.
b) Stabilitet i sidled kan åstadkommas med sidostagning av bågar med hjälp av andra konstruktionsdelar, såsom takåsar tillsammans med krysstagning.

