Hållfasthetslära för skalelement av KL-trä
För ortotropa skalelement kan följande styvhetsmatris ställas upp:
\({C_\rm {KLT}} = \left[ {\begin{array}{*{20}{c}} {{D_{11}}}&{{D_{12}}}&0&0&0&0&0&0\\ {{D_{21}}}&{{D_{22}}}&0&0&0&0&0&0\\ 0&0&{{D_{33}}}&0&0&0&0&0\\ 0&0&0&{{D_{44}}}&0&0&0&0\\ 0&0&0&0&{{D_{55}}}&0&0&0\\ 0&0&0&0&0&{{D_{66}}}&{{D_{67}}}&0\\ 0&0&0&0&0&{{D_{76}}}&{{D_{77}}}&0\\ 0&0&0&0&0&0&0&{{D_{88}}} \end{array}} \right]\)
där:
| [D11 – D33] | beskriver böj- och vridstyvhetsegenskaper (KL-träplatta) |
| [D44 – D55] | beskriver skjuvstyvhetsegenskaper (KL-träplatta) |
| [D66 – D88] | beskriver skivstyvhetsegenskaper (KL-träskiva) |
Böj- och vridstyvhetsegenskaper (KL-träplatta) räknas ofta i kN/m:
\({D_{11}} = \frac{{{E_\rm {0,mean}} \cdot {I_{\rm x,{\rm{net}}}}}}{{1 - {\nu _{{\rm{xy}}}} \cdot {\nu _{{\rm{yx}}}}}}\quad \rm med\quad {\nu _{{\rm{xy}}}} = {\nu _{{\rm{yx}}}} = 0\)
blir ekvationen:
3.90 \({D_{11}} = {E_\rm {0,mean}} \cdot {I_{\rm x,{\rm{net}}}}\)
\({D_{22}} = \frac{{{E_\rm {0,mean}} \cdot {I_{\rm y,{\rm{net}}}}}}{{1 - {\nu _{{\rm{xy}}}} \cdot {\nu _{{\rm{yx}}}}}}\quad \rm med\quad {\nu _{{\rm{xy}}}} = {\nu _{{\rm{yx}}}} = 0\)
blir ekvationen:
3.91 \({D_{22}} = {E_\rm {0,mean}} \cdot {I_{\rm y,{\rm{net}}}}\)
\({D_{33}} = {k_{{\rm{vrid}}}} \cdot {G_\rm {0,mean}}\frac{{b \cdot t_{{\mathop{\rm KLT}\nolimits} }^3}}{{12}}\quad {\rm med}\quad {k_{{\rm{vrid}}}} = 0,65\quad {\rm och}\quad b{\rm{ }} = {\rm{ }}1{\rm{ }}{\mathop{\rm \,m}\nolimits} \)
blir ekvationen:
3.92 \({D_{33}} = 0,65 \cdot {G_\rm {0,mean}}\frac{{t_{{\mathop{\rm KLT}\nolimits} }^3}}{{12}} \cdot 1\;\)
\({D_{12}} = {D_{21}} = \sqrt {{\nu _{{\rm{xy}}}} \cdot {\nu _{{\rm{yx}}}} \cdot {D_{11}} \cdot {D_{22}}} \quad \rm med\quad {\nu _{{\rm{xy}}}} = {\nu _{{\rm{yx}}}} = 0\)
blir ekvationen:
3.93 \({D_{12}} = {D_{21}} = 0\)
Observera:
\({k_{{\rm{vrid}}}} = \left\{ {\begin{array}{*{20}{c}} {0,65{\rm{\;\;för\;KL{\text -}trä\;med\;spalter\;eller\;sprickor.}}}\\ {0,8{\rm{\;\;\;\;för\;KL{\text -}trä\;utan\;spalter\;eller\;sprickor.}}} \end{array}} \right.\)
Skjuvstyvhetsegenskaper (KL-träplatta) räknas ofta i kN/m:
3.94 \({D_{44}} = {\kappa _\rm x} \cdot {G_\rm {0,mean}} \cdot {A_\rm {x,net}}\)
3.95 \({D_{55}} = {\kappa _\rm y} \cdot {G_\rm {0,mean}} \cdot {A_\rm {y,net}}\)
För beräkning och värden på skjuvkorrektionsfaktorerna κx och κy, se avsnitt 3.3.
Skivstyvhetsegenskaper (KL-träskiva) räknas ofta i kN/m:
3.96 \({D_{66}} = {E_\rm {0,mean}} \cdot {A_\rm {x,{\rm{net}}}}\)
3.97 \({D_{77}} = {E_\rm {0,mean}} \cdot {A_\rm {y,{\rm{net}}}}\)
3.98 \({D_{88}} = {G_{{\mathop{\rm S}\nolimits} ,\rm mean}} \cdot {A_\rm {x,{\rm{brutto}}}} = 0,75 \cdot {G_\rm {0,mean}} \cdot {A_\rm {x,{\rm{brutto}}}}\)
GS,mean är skjuvmodulen för hela KL-träelementets tvärsnitt, enligt Silly, 2010
\({D_{67}} = \nu \cdot {D_{66}}\)
och representerar effekten av tvärs utvidgning över längsgående normalkraft, vanligtvis antas ν = 0 och därmed D67 = 0 och på samma sätt D76 = 0.
Verifiering av materialets hållfasthet
Relationen mellan krafter och förskjutningar definieras i matrisform enligt ekvation 3.99 och används med fördel i FEM-beräkningsprogram:
3.99 \(\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{m_x}}\\ {{m_y}} \end{array}}\\ {\begin{array}{*{20}{c}} {{m_{{\mathop{\rm xy}\nolimits} }}}\\ {{n_{{\mathop{\rm xz}\nolimits} }}} \end{array}} \end{array}}\\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{n_{{\mathop{\rm yz}\nolimits} }}}\\ {{n_{\mathop{\rm x}\nolimits} }} \end{array}}\\ {\begin{array}{*{20}{c}} {{n_{\mathop{\rm y}\nolimits} }}\\ {{n_{{\mathop{\rm xy}\nolimits} }}} \end{array}} \end{array}} \end{array}} \right\} = {C_{{\mathop{\rm KLT}\nolimits} }} \cdot \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{K_{\rm{x}}} = \frac{{\partial {\phi _{\mathop{\rm y}\nolimits} }}}{{\partial x}}}\\ {{K_{\rm{y}}} = - \frac{{\partial {\phi _{\mathop{\rm x}\nolimits} }}}{{\partial y}}} \end{array}}\\ {\begin{array}{*{20}{c}} {{K_{{\rm{xy}}}} = \frac{{\partial {\phi _{\mathop{\rm y}\nolimits} }}}{{\partial y}} - \frac{{\partial {\phi _{\mathop{\rm x}\nolimits} }}}{{\partial x}}}\\ {{\gamma _{{\mathop{\rm xz}\nolimits} }} = \frac{{\partial {u_{\mathop{\rm z}\nolimits} }}}{{\partial x}} + {\phi _y}} \end{array}} \end{array}}\\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\gamma _{{\mathop{\rm yz}\nolimits} }} = \frac{{\partial {u_{\mathop{\rm z}\nolimits} }}}{{\partial y}} - {\phi _x}}\\ {{\varepsilon _{\mathop{\rm x}\nolimits} } = \frac{{\partial {u_{\mathop{\rm x}\nolimits} }}}{{\partial x}}} \end{array}}\\ {\begin{array}{*{20}{c}} {{\varepsilon _{\mathop{\rm y}\nolimits} } = \frac{{\partial {u_{\mathop{\rm y}\nolimits} }}}{{\partial y}}}\\ {{\gamma _{{\mathop{\rm xy}\nolimits} }} = \frac{{\partial {u_{\mathop{\rm x}\nolimits} }}}{{\partial y}} - \frac{{\partial {u_{\mathop{\rm y}\nolimits} }}}{{\partial x}}} \end{array}} \end{array}} \end{array}} \right\}\)
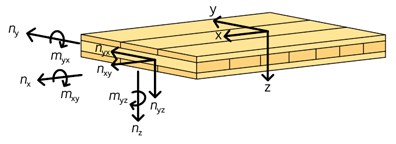
φ och u representerar rotation respektive förskjutning av elementytans tyngdpunktscentrum i riktningar enligt figur 3.28.
Utifrån ekvation 3.99 erhålls både krafter och deformationer och utifrån detta kan spänningar i materialet beräknas.

Montage av Portvakten, Växjö.
Böjmoment kring x-axeln och y-axeln
\({m_{{\mathop{\rm x}\nolimits} ,\rm E,d}} \le {m_\rm {x,R,d}}\)
| mx,E,d | är dimensionerande böjmoment i kNm/m. |
| mx,R,d | är dimensionerande bärförmåga för böjmoment i kNm/m och beräknas: |
\({m_\rm {x,R,d}} = {W_\rm {x,{\rm{net}}}} \cdot {f_\rm {m,xlay,d}}\)
\({m_\rm {y,E,d}} \le {m_\rm {y,R,d}}\)
| my,E,d | är dimensionerande böjmoment i kNm/m. |
| my,R,d | är dimensionerande bärförmåga för böjmoment i kNm/m och beräknas: |
\({m_\rm {y,R,d}} = {W_\rm {y,{\rm{net}}}} \cdot {f_\rm {m,ylay,d}}\)
Tvärkraft i xz-planet och yz-planet
\({n_{{\mathop{\rm xz}\nolimits} ,\rm E,d}} \le {n_\rm {xz,R,d}}\)
| nxz,E,d | är dimensionerande tvärkraft i kN/m. |
| nxz,R,d | är dimensionerande bärförmåga för tvärkraft i kN/m och beräknas: |
\({n_\rm {xz,R,d}} = \frac{{{I_\rm {x,{\rm{net}}}} \cdot {\rm{1\,m}}}}{{{S_{{\rm{R}},x,{\rm{net}}}}}}{f_\rm {v,9090,ylay,d}}\)
\({n_{{\mathop{\rm yz}\nolimits} ,\rm E,d}} \le {n_\rm {yz,R,d}}\)
| nyz,E,d | är dimensionerande tvärkraft i kN/m. |
| nyz,R,d | är dimensionerande bärförmåga för tvärkraft i kN/m och beräknas: |
\({n_\rm {yz,R,d}} = \frac{{{I_{y,{\rm{net}}}} \cdot {\rm{1\,m}}}}{{{S_{{\rm{R}},\rm y,{\rm{net}}}}}}{f_\rm {v,9090,xlay,d}}\)
Vridmoment i xy-planet eller yx-planet
\({m_\rm {xy,E,d}} \le {m_\rm {xy,R,d}}\)
| mxy,E,d | är dimensionerande vridmoment i kNm/m. |
| mxy,R,d | är dimensionerande bärförmåga för vridmoment i kNm/m och beräknas: |
\({m_\rm {xy,R,d}} = {W_\rm {tor,x,{\rm{KLT}}}} \cdot {f_\rm {tor,d}}\)
Observera: mxy = myx om bx = by
Normalkraft i x-riktning och y-riktning
\({n_{{\mathop{\rm x}\nolimits} ,\rm E,d}} \le {n_\rm {x,R,d}}\)
| nx,E,d | är dimensionerande normalkraft i kN/m. |
| nx,R,d | är dimensionerande bärförmåga för normalkraft i kN/m och beräknas: |
\({n_\rm {x,R,d}} = {A_{\rm x,{\rm{net}}}} \cdot {f_\rm {t,xlay,d}}\)
för dragspänning och
\({n_\rm {x,R,d}} = {A_{\rm x,{\rm{net}}}} \cdot {f_\rm {c,xlay,d}}\)
för tryckspänning.
\({n_{{\mathop{\rm y}\nolimits} ,\rm E,d}} \le {n_{{\mathop{\rm y}\nolimits} ,\rm R,d}}\)
| ny,E,d | är dimensionerande normalkraft i kN/m. |
| ny,R,d | är dimensionerande bärförmåga för normalkraft i kN/m och beräknas: |
\({n_\rm {y,R,d}} = {A_{\rm y,{\rm{net}}}} \cdot {f_\rm {t,ylay,d}}\)
för dragspänning och
\({n_\rm {y,R,d}} = {A_{\rm y,{\rm{net}}}} \cdot {f_\rm {c,ylay,d}}\)
för tryckspänning.
Tvärkraft i xy-planet eller yx-planet
\({n_{{\mathop{\rm xy}\nolimits} ,\rm E,d}} \le {n_\rm {xy,R,d}}\)
| nxy,E,d | är dimensionerande tvärkraft i KL-träskivans plan i kN/m. |
| nxy,R,d | är dimensionerande bärförmåga för tvärkraft i kN/m. |
\({n_\rm {xy}} = {n_\rm {yx}}\)