En vertikalt belastad yttervägg på första våningen i en tvåvåningsbyggnad har höjden \(l\)e = 2,95 m och bredden b0 = 4,54 m. Väggen har två fönster och effektiv väggbredd utan fönster är bef = 2,40 m, se figur 6.21 och figur 6.22.
Dimensionerande last från tak, vägg och bjälklag ovanför väggen är Fd = 30 kN/m. Vindtryck tvärs väggen är qd = 2,4 kN/m2.
Väggen består av en 3-skiktsskiva av KL-trä, med tjockleken 3 × 30 = 90 mm och med samtliga skikt av brädor i hållfasthetsklass C24. Klimatklass 1, säkerhetsklass 3 (γd = 1).
För KL-trä med enbart brädor i hållfasthetsklass C24 gäller enligt tabell 3.7:
E0,x,0,05 = 7 400 MPa
E0,x,mean = 11 000 MPa
G9090,xlay,mean = 50 MPa
G090,xlay,mean = 690 MPa
Enligt tabell 3.6 gäller:
fm,k = 24 MPa
fc,0,k = 21 MPa
Med γM = 1,25 enligt tabell 3.2 och kmod = 0,9 enligt tabell 3.3 (vindlast huvudlast = korttidslast) blir dimensionerande hållfastheter:
\({f_{{\rm{m}},{\rm{d}}}} = \frac{{{k_{{\rm{mod}}}} \cdot {f_{{\rm{m}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}} = \frac{{0,9 \cdot 24}}{{1,25}} = 17,28\;{\rm{MPa}}\)
\({f_{{\rm{c}},0,{\rm{d}}}} = \frac{{{k_{{\rm{mod}}}} \cdot {f_{{\rm{c}},0,{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}} = \frac{{0,9 \cdot 21}}{{1,25}} = 15,12\;{\rm{MPa}}\)
Beräkningar:
Tvärsnittsstorheter för olika dimensioner för 3-skiktsskivor av KL-trä finns i tabell 3.11 samt i tabell 3.13 för KL-träskivor med brädor i hållfasthetsklass C24. Tvärsnittsegenskaper kan också beräknas för en strimla bx = 1,0 m av skivan, se tabell 6.9.
Knäckning kontrolleras i brottgränstillstånd:
\(\frac{{{\sigma _{{\rm{c}},0,{\rm{d}}}}}}{{{k_\rm {c,y}} \cdot \;{f_{{\rm{c}},0,{\rm{d}}}}}} + \frac{{{\sigma _{{\rm{m}},{\rm{d}}}}}}{{\;{f_{{\rm{m}},{\rm{d}}}}}} \le 1\)
Reduktionsfaktorn kc,y kan skrivas som:
\({k_{{\rm{c}},{\rm{y}}}} = \frac{1}{{{k_{\rm{y}}} + \sqrt {k_{\rm{y}}^2 - \lambda _{{\rm{rel}},{\rm{y}}}^2} }} = \frac{1}{{1,971 + \sqrt {{{1,971}^2} - {{1,675}^2}} }} = 0,332\)
där:
\({k_{\rm{y}}} = 0,5\left( {1 + 0,1\left( {{\lambda _{{\rm{rel}},{\rm{y}}}} - 0,3} \right) + \lambda _{{\rm{rel}},{\rm{y}}}^2} \right) =\\ = 0,5\left( {1 + 0,1\left( {1,675 - 0,3} \right) + {{1,675}^2}} \right) = 1,971\)
där:
\({\lambda _{{\rm{rel}},{\rm{y}}}} = \frac{{{\lambda _{\rm{y}}}}}{\pi }\sqrt {\frac{{\;{f_{{\rm{c}},0,{\rm{k}}}}}}{{{E_{0,05}}}}} = \frac{{98,8}}{\pi }\sqrt {\frac{{21}}{{7400}}} = 1,675\)
Vid öppningar i väggen erhålls större belastning på de återstående väggdelarna. I regel kan man räkna med jämnt utbredd last på väggdelar mellan fönster. Laster fördelas till effektiva bredden bef med faktor fb:
\({f_{\rm{b}}} = \frac{{{b_0}}}{{{b_{{\rm{ef}}}}}} = \frac{{4,54}}{{2,40}} = 1,89\)
Vertikala lasten beräknas för en 1,0 m strimla av effektiva bredden bef:
\({N_{\rm{d}}} = {b_{\rm{x}}} \cdot {f_{\rm{b}}} \cdot {P_{\rm{d}}} = 1,0 \cdot 1,89 \cdot 30 = 57\;{\rm{kN}}\)
Moment av vindlasten:
\({M_{{\rm{y}},{\rm{d}}}} = \frac{{{q_{\rm{d}}} \cdot {l_{\rm{e}}}^2}}{8} = \frac{{2,4 \cdot 1,89 \cdot {{2,95}^2}}}{8} = 4,93\;{\rm{kNm}}\)
\(\frac{{{\sigma _{{\rm{c}},0,{\rm{d}}}}}}{{{k_\rm {c,y}} \cdot \;{f_{{\rm{c}},0,{\rm{d}}}}}} + \frac{{{\sigma _{{\rm{m}},{\rm{d}}}}}}{{\;{f_{{\rm{m}},{\rm{d}}}}}} = \frac{{{N_{\rm{d}}}}}{{{k_\rm {c,y}} \cdot {A_{{\rm{x}},{\rm{net\;}}}} \cdot \;{f_{{\rm{c}},0,{\rm{d}}}}}} + \frac{{{M_{{\rm{y}},{\rm{d}}}}}}{{{W_{{\rm{x}},{\rm{net\;}}}} \cdot \;{f_{{\rm{m}},{\rm{d}}}}}} =\)
\(= \frac{{57 \cdot {{10}^3}}}{{0,332 \cdot 600 \cdot {{10}^2} \cdot 13,44}} + \frac{{4,93 \cdot {{10}^6}}}{{1300 \cdot {{10}^3} \cdot 15,36}} = 0,213 + 0,247 = 0,460 \le 1 \) OK
Väggen klarar tryck- och momentbelastningen, utnyttjandegraden är 46 procent.
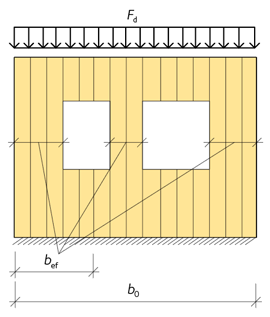
Figur 6.21 Väggskiva med öppningar.
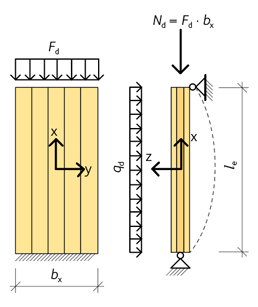
Figur 6.22 Del av väggskiva.
Tabell 6.9 Egenskaper för 3-skikts symmetrisk skiva av KL-trä, strimla med bredd bx = 1,05 m. Skivtjocklek 90 mm (30/30/30).
| Egenskap | Beräkningsformel |
| Tyngdpunktscentrum (mm) |
\({z_{\rm{s}}} = \frac{{{h_{{\rm{KLT}}}}\;}}{2}\) |
| Tvärsnittsarean (mm2) |
\({A_{\rm x{\rm ,net}}} = {b_{\mathop{\rm x}\nolimits} }\cdot2\cdot{t_1}\) |
| Nettotröghetsmoment (mm4) |
\(\begin{array}{c} {I_{{\rm{x}},{\rm{net}}}} = {b_{\rm{x}}}\left( {\frac{{t_1^3}}{{12}} + {t_1}{a_1}^2 + \frac{{t_3^3}}{{12}} + {t_3}{a_3}^2} \right) = \\ = {b_{\rm{x}}}\left( {2 \cdot \frac{{t_1^3}}{{12}} + 2 \cdot {t_1}{a_1}^2} \right) \end{array}\) |
| Nettoböjmotstånd (mm3) |
\({W_{{\rm{x}},{\rm{net}}}} = \frac{{{I_{{\rm{x}},{\rm{net}}}}}}{{{z_{\rm{s}}}}}\) |
| Gammavärden | \({\gamma _1} = 1;\quad {\gamma _3} = \frac{1}{{1 + \frac{{{\pi ^2}{E_{{\rm{x}},3}}{t_3}}}{{l_{\rm{e}}^2}}\;\frac{{{t_2}}}{{{G_{9090,2}}}}}}\) |
| Effektivt böjmotstånd (mm4) |
\(\begin{array}{c} {I_{{\rm{x}},{\rm{ef}}}} = \frac{{{b_{\rm{x}}}t_1^3}}{{12}} + {b_{\rm{x}}}{t_1}{a_1}^2 + \frac{{{b_{\rm{x}}}t_3^3}}{{12}} + {\gamma _3}{b_{\rm{x}}}{t_3}{a_3}^2 = \\ = {b_{\rm{x}}} \cdot \left( {\frac{{2 \cdot t_1^3}}{{12}} + \left( {1 + {\gamma _3}} \right){t_1}{a_1}^2} \right) \end{array}\) |
| Effektiv tröghetsradie ix,ef |
\({i_{{\rm{x}},{\rm{ef}}}} = \sqrt {\frac{{{I_{x,{\rm{ef}}}}}}{{{A_{x,{\rm{net}}}}}}} \) |
| Slankhetsfaktor λy | \({\lambda _{\rm{y}}} = \frac{{{l_{\rm{e}}}}}{{{i_{{\rm{x}},{\rm{ef}}}}}}\)/ |
| Egenskap | Tillämpning i exemplet |
| Tyngdpunktscentrum (mm) |
\({z_{\rm{s}}} = \frac{{90\;}}{2} = 45\;{\rm{mm}}\) |
| Tvärsnittsarean (mm2) |
\({A_{\rm x{\rm ,net}}} = 1000 \cdot 2 \cdot 30 = 600 \cdot {10^2}\;{\rm{m}}{{\rm{m}}^2}\) |
| Nettotröghetsmoment (mm4) |
\(\begin{array}{c} {I_{{\rm{x}},{\rm{net}}}} = 1000\left( {2 \cdot \frac{{{{30}^3}}}{{12}} + 2 \cdot 30 \cdot {{30}^2}} \right) = \\ = 5850 \cdot {10^4}\;{\rm{m}}{{\rm{m}}^4} \end{array}\) |
| Nettoböjmotstånd (mm3) |
\({W_{{\rm{x}},{\rm{net}}}} = \frac{{5850 \cdot {{10}^4}}}{{45}} = 1300 \cdot {10^3}\;{\rm{m}}{{\rm{m}}^3}\) |
| Gammavärden | \({\gamma _1} = 1;\quad {\gamma _3} = \frac{1}{{1 + \frac{{{\pi ^2}11000 \cdot 30}}{{{{2950}^2}}}\;\frac{{30}}{{50}}}} = 0,817\) |
| Effektivt böjmotstånd (mm4) |
\(\begin{array}{c} {I_{{\rm{x}},{\rm{ef}}}} = 1000 \cdot \left( {\frac{{2 \cdot {{30}^3}}}{{12}} + \left( {1 + 0,817} \right) \cdot 30 \cdot {{30}^2}} \right) = \\ = 5356 \cdot {10^4}\;{\rm{m}}{{\rm{m}}^4} \end{array}\) |
| Effektiv tröghetsradie ix,ef |
\({i_{{\rm{x}},{\rm{ef}}}} = \sqrt {\frac{{5356 \cdot {{10}^4}}}{{600\cdot{{10}^2}}}} = 29,87\;{\rm{mm}}\) |
| Slankhetsfaktor λy | \({\lambda _{\rm{y}}} = \frac{{2950}}{{29,87}} = 98,8\) |

