Kontroll av dragspänning i KL-träskivans plan
För en KL-träskiva utsatt för dragning parallellt med ytskiktet, se figur 3.13, gäller ekvation 3.43:
3.43 \({\sigma _{{\rm{t}},{\rm{x}},{\rm{d}}}} = \;\frac{{{F_{{\rm{t}},{\rm{x}},{\rm{d}}}}}}{{{A_{{\rm{x}},{\rm{net}}}}\;}}\; \le \;{f_{{\rm{t}},0,{\rm{xlay}},{\rm{d}}}} = \;{k_{{\rm{sys}}}} \cdot {k_{{\rm{mod}}}}\frac{{{f_{{\rm{t}},0,{\rm{xlay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Ft,x,d | är dimensionerande dragkraft i x-riktningen. |
| Ax,net | är tvärsnittets verksamma nettoarea i x-riktningen. |
| ft,0,xlay,d | är dimensionerande draghållfasthet för brädor i x-riktningen. |
| ft,0,xlay,k | är karakteristisk draghållfasthet för brädor i x-riktningen. |
| ksys | är en systemfaktor, se avsnitt 3.1.6. |
| kmod | är en modifikationsfaktor, se avsnitt 3.1.5. |
| γM | är partialkoefficienten för materialet, se avsnitt 3.1.5. |
För en KL-träskiva utsatt för dragning vinkelrätt mot ytskiktet, se figur 3.14, gäller ekvation 3.44:
3.44 \({\sigma _{{\rm{t}},{\rm{y}},{\rm{d}}}} = \;\frac{{{F_{{\rm{t}},{\rm{y}},{\rm{d}}}}}}{{{A_{{\rm{y}},{\rm{net}}}}\;}} \le {f_{{\rm{t}},0,{\rm{ylay}},{\rm{d}}}} = \;{k_{{\rm{sys}}}} \cdot {k_{{\rm{mod}}}}\frac{{{f_{{\rm{t}},0,{\rm{ylay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Ft,y,d | är dimensionerande dragkraft i y-riktningen. |
| Ay,net | är tvärsnittets verksamma nettoarea i y-riktningen. |
| ft,0,ylay,d | är dimensionerande draghållfasthet för brädor i y-riktningen. |
| ft,0,ylay,k | är karakteristisk draghållfasthet för brädor i y-riktningen. |
Kontroll av tryckspänning i KL-träskivans plan då risk för knäckning inte föreligger
För en KL-träskiva utsatt för tryck parallellt med ytskiktet, se figur 3.15, gäller ekvation 3.45:
3.45 \({\sigma _{{\rm{c}},{\rm{x}},{\rm{d}}}} = {\rm{\;}}\frac{{{F_{{\rm{c}},{\rm{x}},{\rm{d}}}}}}{{{A_{{\rm{x}},{\rm{net}}}}{\rm{\;}}}}{\rm{\;}} \le \;{f_{{\rm{c}},0,{\rm{xlay}},{\rm{d}}}} = {\rm{\;}}{k_{{\rm{mod}}}}\frac{{{f_{{\rm{c}},0,{\rm{xlay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Fc,x,d | är dimensionerande tryckkraft i x-riktningen. |
| Ax,net | är tvärsnittets verksamma nettoarea i x-riktningen. |
| fc,0,xlay,d | är dimensionerande tryckhållfasthet för brädor i x-riktningen. |
| fc,0,xlay,k | är karakteristisk tryckhållfasthet för brädor i x-riktningen. |
| kmod | är en modifikationsfaktor, se avsnitt 3.1.5. |
| γM | är partialkoefficienten för materialet, se avsnitt 3.1.5. |
För en KL-träskiva utsatt för tryck vinkelrätt mot ytskiktet, se figur 3.16, gäller ekvation 3.46:
3.46 \({\sigma _{{\rm{c}},{\rm{y}},{\rm{d}}}} = {\rm{\;}}\frac{{{F_{{\rm{c}},{\rm{y}},{\rm{d}}}}}}{{{A_{{\rm{y}},{\rm{net}}}}{\rm{\;}}}}{\rm{\;}} \le \;{f_{{\rm{c}},0,{\rm{ylay}},{\rm{d}}}} = {\rm{\;}}{k_{{\rm{mod}}}}\frac{{{f_{{\rm{c}},0,{\rm{ylay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Fc,y,d | är dimensionerande tryckkraft i y-riktningen. |
| Ay,net | är tvärsnittets verksamma nettoarea i y-riktningen. |
| fc,0,ylay,d | är dimensionerande tryckhållfasthet för brädor i y-riktningen. |
| fc,0,ylay,k | är karakteristisk tryckhållfasthet för brädor i y-riktningen. |
Kontroll av tryckspänning vinkelrätt KL-träskivans plan
För en KL-träskiva som påverkas av tryck vinkelrätt mot dess plan, se figur 3.17, gäller ekvation 3.47:
3.47 \({\sigma _{{\rm{c}},{\rm{z}},{\rm{d}}}} = {\rm{\;}}\frac{{{F_{{\rm{c}},{\rm{z}},{\rm{d}}}}}}{{{A_{{\rm{ef}}}}{\rm{\;}}}}{\rm{\;}} \le \;{f_{{\rm{c}},90,{\rm{xlay}},{\rm{d}}}} = {k_{{\rm{c}},90}} \cdot {k_{{\rm{mod}}}}\frac{{{f_{{\rm{c}},90,{\rm{xlay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Fc,z,d | är dimensionerande tryckkraft vinkelrätt mot fiberriktningen. |
| Aef | är effektiv kontaktarea vid tryck vinkelrätt mot fiberriktningen. |
| fc,90,xlay,d | är dimensionerande tryckhållfasthet vinkelrätt mot fiberriktningen. |
| fc,90,xlay,k | är karakteristisk tryckhållfasthet vinkelrätt mot fiberriktningen. |
| kc,90 | är en faktor som tar hänsyn till hur lasten angriper och graden av sammantryckning. |
| kmod | är en modifikationsfaktor, se avsnitt 3.1.5. |
| γM | är partialkoefficienten för materialet, se avsnitt 3.1.5. |
Effektiv kontaktyta samt kc,90-faktorn beror av lastens placering, se figur 3.18, och det pågår arbete med att fastställa värden för kc,90. Hittills genomförda provningar visar att värden enligt tabell 3.16 kan tillämpas.
Kontroll av böjspänning i KL-träskivans plan
För en KL-träskiva eller KL-träplatta som påverkas av böjmoment kring sin y-axel, se figur 3.19, gäller ekvation 3.48:
3.48 \({\sigma _{{\rm{m}},{\rm{y}},{\rm{d}}}} = {\rm{\;}}\frac{{{M_{{\rm{y}},{\rm{d}}}}}}{{{W_{{\rm{x}},{\rm{net\;}}}}}} \le {f_{{\rm{m}},{\rm{xlay}},{\rm{d}}}} = {\rm{\;}}{k_{{\rm{sys}}}} \cdot {k_{{\rm{mod}}}}\frac{{{f_{{\rm{m}},{\rm{xlay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| My,d | är dimensionerande moment kring y-axeln. |
| Wx,net | är skivans nettoböjmotstånd. |
| fm,0,xlay,d | är dimensionerande böjhållfasthet. |
| fm,0,xlay,k | är karakteristisk böjhållfasthet. |
| ksys | är en systemfaktor, se avsnitt 3.1.6. |
| kmod | är en modifikationsfaktor, se avsnitt 3.1.5. |
| γM | är partialkoefficienten för materialet, se avsnitt 3.1.5. |
För en KL-träskiva eller KL-träplatta som påverkas av böjmoment kring sin x-axel, se figur 3.20, gäller ekvation 3.49:
3.49 \({\sigma _{{\rm{m}},{\rm{x}},{\rm{d}}}} = {\rm{\;}}\frac{{{M_{{\rm{x}},{\rm{d}}}}}}{{{W_{{\rm{y}},{\rm{net\;}}}}}} \le {f_{{\rm{m}},{\rm{ylay}},{\rm{d}}}} = {\rm{\;}}{k_{{\rm{sys}}}} \cdot {k_{{\rm{mod}}}}\frac{{{f_{{\rm{m}},{\rm{ylay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Mx,d | är dimensionerande moment kring x-axeln. |
| Wy,net | är skivans nettoböjmotstånd. |
| fm,ylay,d | är dimensionerande böjhållfasthet. |
| fm,ylay,k | är karakteristisk böjhållfasthet. |
Kontroll av böjspänning i KL-träväggskiva eller KL-träbalk
För en KL-träväggskiva eller KL-träbalk som påverkas av ett böjmoment kring sin z-axel, se figur 3.21, gäller i x-riktningen ekvation 3.50:
3.50 \({\sigma _{{\rm{m}},{\rm{z}},{\rm{d}}}} = {\rm{\;}}\frac{{{M_{{\rm{z}},{\rm{d}}}}}}{{{W_{{\rm{z}},{\rm{x}},{\rm{net\;}}}}}} \le {f_{{\rm{m}},{\rm{xlay}},{\rm{d}}}} = {k_{{\rm{mod}}}}\frac{{{f_{{\rm{m}},{\rm{xlay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Mz,d | är dimensionerande moment kring z-axeln. |
| Wz,x,net | är skivans nettoböjmotstånd. |
| fm,xlay,d | är dimensionerande böjhållfasthet. |
| fm,xlay,k | är karakteristisk böjhållfasthet. |
\({W_{{\rm{z}},{\rm{x}},{\rm{net\;}}}} = \;\frac{{\mathop \sum \nolimits^ {t_{\rm{i}}} \cdot {h^2}}}{6} = \frac{{\left( {{t_1} + {t_3} + \ldots } \right) \cdot {h^2}}}{6}\)
där:
| ti | är tjockleken för brädor i x-riktningen. |
| h | är hela KL-träskivans eller KL-träbalkens höjd. |
För en KL-träväggskiva eller KL-träbalk som påverkas av ett böjmoment kring sin z-axel enligt figur 3.22 gäller i y-riktningen ekvation 3.51:
3.51 \({\sigma _{{\rm{m}},{\rm{z}},{\rm{d}}}} = {\rm{\;}}\frac{{{M_{{\rm{z}},{\rm{d}}}}}}{{{W_{{\rm{z}},{\rm{y}},{\rm{net\;}}}}}} \le {f_{{\rm{m}},{\rm{ylay}},{\rm{d}}}} = {k_{{\rm{mod}}}}\frac{{{f_{{\rm{m}},{\rm{ylay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Mz,d | är dimensionerande moment kring z-axeln. |
| Wz,y,net | är skivans nettoböjmotstånd. |
| fm,ylay,d | är dimensionerande böjhållfasthet. |
| fm,ylay,k | är karakteristisk böjhållfasthet. |
3.52 \({W_{{\rm{z}},{\rm{y}},{\rm{net\;}}}} = \;\frac{{\mathop \sum \nolimits^ {t_{\rm{i}}}{h^2}}}{6} = \frac{{\left( {{t_2} + {t_4} + \ldots } \right) \cdot {h^2}}}{6}\)
där:
| ti | är tjockleken för brädor i y-riktningen. |
| h | är hela KL-träskivans eller KL-träbalkens höjd. |
Med ett litet förhållande mellan KL-träskiv- eller -balklängd, L, och höjd, h, gäller inte balkteorin med linjära spänningsfördelningar. Avvikelse blir märkbar från L / h ≤ 4.
Kombinerad böjning i två riktningar
För KL-träplattor som används till bärande tak eller likartade konstruktioner utan bucklingsrisk kan det uppkomma böjspänningar i planet i samma riktning och verifiering av hållfasthet ska göras enligt ekvation 3.53:
3.53 \(\frac{{{\sigma _{{\rm{m}},{\rm{y}},{\rm{d}}}}}}{{{f_{{\rm{m}},{\rm{xlay}},{\rm{d}}}}}} + \frac{{{\sigma _{{\rm{m}},{\rm{z}},{\rm{d}}}}}}{{{f_{{\rm{m}},{\rm{xlay}},{\rm{d}}}}}} \le 1\)
där:
| σm,y,d och σm,z,d | är dimensionerande böjspänning kring huvudaxlarna. |
| fm,xlay,d | är motsvarande böjhållfastheter. |
3.54 \(\frac{{{M_{{\rm{y}},{\rm{d}}}}}}{{{W_{{\rm{x}},{\rm{net\;}}}}{f_{{\rm{m}},\rm xlay,{\rm{d}}}}}} + \frac{{{M_{{\rm{z}},{\rm{d}}}}}}{{{W_{{\rm{z}},{\rm{x}},{\rm{net\;}}}}{f_{{\rm{m}},{\rm{xlay}},{\rm{d}}}}}} \le 1\)
där:
| My,d och Mz,d | är dimensionerande moment kring huvudaxlarna. |
| Wx,net och Wz,x,net | är motsvarande nettoböjmotstånd. |
Kontroll av skjuvspänning vinkelrätt mot planet
För KL-träskivor utsatta för tvärkrafter vinkelrätt mot KL-träskivan uppkommer skjuvspänningar. Eftersom KL-träskivan består av brädor i längsled respektive i tvärled bör båda riktningarna kontrolleras. Skjuvhållfastheten (rullskjuvhållfasthet) tvärs fiberriktningen är ofta betydligt lägre än längs fiberriktningen.
För en 5-skiktsskiva eller balk av KL-trä som påverkas av tvärkrafter, Vxz,d, respektive Vyz,d, se figur 3.23 och figur 3.24, gäller följande:
- a) Verifiering av skjuvningen parallellt med fiberriktningen i skikt 3 i figur 3.23 och skikt 2 eller 4 i figur 3.24:
3.55 \({\tau _{{\rm{v}},{\rm{xz}},{\rm{d}}}} = {\rm{\;}}\frac{{{S_{{\rm{x}},{\rm{net}}}} \cdot {V_{{\rm{xz}},{\rm{d}}}}}}{{{I_{{\rm{x}},{\rm{net}}}} \cdot {b_{\rm{x}}}}}{\rm{\;}} \le \;{f_{{\rm{v}},090,{\rm{ylay}},{\rm{d}}}} = {\rm{\;}}{k_{{\rm{mod}}}}\frac{{{f_{{\rm{v}},090,{\rm{ylay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
Vxz,d är dimensionerande tvärkraft. Sx,net är skivans nettostatiska moment. fv,090,ylay,d är dimensionerande längsskjuvhållfasthet för brädor. fv,090,ylay,k är karakteristisk längsskjuvhållfasthet för brädor. kmod är en modifikationsfaktor, se avsnitt 3.1.5. γM är partialkoefficienten för materialet, se avsnitt 3.1.5. - b) Verifiering av rullskjuvningen (skjuvning tvärs fiberriktningen) i skikt 2 eller 4 i figur 3.23 och i skikt 3 i figur 3.24:
3.56 \({\tau _{{\rm{Rv}},{\rm{yz}},{\rm{d}}}} = {\rm{\;}}\frac{{{S_{{\rm{R}},{\rm{y}},{\rm{net}}}} \cdot {V_{{\rm{yz}},{\rm{d}}}}}}{{{I_{y,{\rm{net}}}} \cdot {b_{\rm{y}}}}}{\rm{\;}} \le \;{f_{{\rm{v}},9090,{\rm{xlay}},{\rm{d}}}} = {\rm{\;}}{k_{{\rm{mod}}}}\frac{{{f_{{\rm{v}},9090,{\rm{xlay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
Vyz,d är dimensionerande tvärkraft. SR,y,net är skivans nettostatiska moment. fv,9090,xlay,d är dimensionerande rullskjuvhållfasthet för brädor. fv,9090,xlay,k är karakteristisk rullskjuvhållfasthet för brädor.
Vid dimensionering av KL-trä behöver inte hänsyn tas till sprickor i KL-träskivorna då uppbyggnad med skikt av korsvis limmade brädor förhindrar och minimerar risken för uppkomst och spridning av sprickor. För konstruktioner med liten skivbredd b och under vissa omständigheter kan den behöva reduceras med faktorn kcr = 0,67, genom ekvation bef = kcr ∙ b.
Kontroll av skjuvhållfasthet i KL-träskivans plan
KL-träskivor används ofta i stabiliserande konstruktioner. Exempelvis medför vindlaster som tas upp av stabiliserande skivor att tvärkrafter Vxy och Vyx uppkommer i KL-träskivans plan. Då KL-träskivorna kan ta last i flera riktningar bör hållfastheten kontrolleras med avseende på hela KL-träskivan, panelskjuvning, och ingående skikt i KL-träskivan, skiktskjuvning. Dessutom måste hänsyn tas till om brädorna är limmade på kanterna och om det finns sprickor i brädorna längs med fibrerna. Beroende på kantlimning och sprickbildning varierar skjuvhållfastheten i KL-träskivans plan.
Här anges hållfasthet för KL-träskivor utan kantlimmade brädor eller med spruckna brädor.
Vid kontroll av hela KL-träskivan, det vill säga panelskjuvning, se figur 3.25, gäller ekvation 3.57 och 3.58:
3.57 \({\tau _{{\rm{v}},{\rm{xy}},{\rm{d}}}} = {\rm{\;}}\frac{{{V_{{\rm{xy}},{\rm{d}}}}}}{{{A_{{\rm{x}},{\rm{net}}}}}}{\rm{\;}} \le \;{f_{{\rm{v}},090,{\rm{xlay}},{\rm{d}}}} = {\rm{\;}}{k_{\bmod }}\frac{{{f_{{\rm{v}},090,{\rm{xlay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Vxy,d | är dimensionerande tvärkraft. |
| Ax,net | är skivans verksamma area. |
| fv,090,xlay,d | är dimensionerande längsskjuvhållfasthet. |
| fv,090,xlay,k | är karakteristisk längsskjuvhållfasthet. |
| kmod | är en modifikationsfaktor, se avsnitt 3.1.5. |
| γM | är partialkoefficienten för materialet, se avsnitt 3.1.5. |
och:
3.58 \({\tau _{{\rm{v}},{\rm{yx}},{\rm{d}}}} = {\rm{\;}}\frac{{{V_{{\rm{yx}},{\rm{d}}}}}}{{{A_{{\rm{y}},{\rm{net}}}}}}{\rm{\;}} \le \;{f_{{\rm{v}},090,{\rm{ylay}},{\rm{d}}}} = {\rm{\;}}{k_{{\rm{mod}}}}\frac{{{f_{{\rm{v}},090,{\rm{ylay}},{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Vyx,d | är dimensionerande tvärkraft. |
| Ay,net | är skivans verksamma area. |
| fv,090,ylay,d | är dimensionerande längsskjuvhållfasthet. |
| fv,090,ylay,k | är karakteristisk längsskjuvhållfasthet. |
Notera att skjuvspänningar i KL-träskivor fördelas jämnt över nettotvärsnittet och inte kvadratiskt, varför skjuvspänningen beräknas utan faktorn 1,5 som används för rektangulärt tvärsnitt när balkteorin gäller.
Korslimning av skikten medför att skjuvspänningen i förhållande till skikttjocklek blir enligt ekvation 3.59:
3.59 \({\tau _{{\rm{v}},{\rm{xy}}}} \cdot {h_x} = {\tau _{{\rm{v}},{\rm{yx}}}} \cdot {h_y}\)
med:
3.60 \({h_{\rm{x}}} = \mathop \sum \nolimits^ \frac{{{E_{{\rm{x}},{\rm{i}}}}}}{{{E_{\rm ref}}}}{t_{\rm{i}}}\)
och:
3.61 \({h_{\rm{y}}} = \mathop \sum \nolimits^ \frac{{{E_{{\rm{y}},{\rm{i}}}}}}{{{E_{\rm ref}}}}{t_{\rm{i}}}\)
Skjuvning mellan skikten, se figur 3.26, för en KL-träskiva bestäms av hållfastheten hos limfogarna mellan tvärgående och längsgående brädor. Skjuvspänningen kan skrivas enligt ekvation 3.62:
3.62 \({\tau _{{\rm{mz}},{\rm{d}}}} = {\rm{\;}}\frac{{{M_{{\rm{t}},{\rm{d}}}}}}{{{n_{\rm{t}}} \cdot {W_{\rm{p}}}}}{\rm{\;}} \le \;{f_{{\rm{mz}},9090,{\rm{d}}}} = {\rm{\;}}{k_{{\rm{mod}}}}\frac{{{f_{{\rm{mz}},9090,{\rm{k}}}}}}{{{\gamma _{\rm{M}}}}}\)
där:
| Mt,d | är dimensionerande moment. |
| Wp | är skivans polära tröghetsmoment. |
| nt | är antalet limmade ytor i skivan. |
| fmz,9090,d | är dimensionerande skjuvhållfasthet. |
| fmz,9090,k | är karakteristisk skjuvhållfasthet. |
Exempelvis gäller ekvation 3.63 för en 3-skiktsskiva av KL-trä enligt figur 3.26, för beräkning av vridande moment i planen:
3.63 \({M_{{\rm{t}},{\rm{d}}}} = {V_{{\rm{x}},{\rm{d}}}} \cdot l\)
där:
| l | är avståndet mellan vridcentrumet och kraften, Vx,d. |
| nt | är antalet limmade ytor av storlek bl,x ∙ bl,y. |
I detta fall blir nt = 2 limskikt · 5 brädor i x-led · 5 brädor i y-led = 50.
Polära tröghetsmomentet kan skrivas enligt ekvation 3.64:
3.64 \({W_{\rm{p}}} = \frac{{2 \cdot {I_{\rm{p}}}}}{{\sqrt {{b_{{\rm{l}},{\rm{x}}}}{b_{{\rm{l}},{\rm{y}}}}} }}\)
med:
3.65 \({I_{\rm{p}}} = {I_1} + {I_2} = \frac{{{b_{{\rm{l}},{\rm{x}}}} \cdot {b_{{\rm{l}},{\rm{y}}}}^3}}{{12}} + \frac{{{b_{{\rm{l}},{\rm{x}}}}^3 \cdot {b_{{\rm{l}},{\rm{y}}}}}}{{12}}\)
och med bl,x och bl,y för lamellernas bredd i x- respektive y-riktning.
För kvadratiska limmade ytor, bl,x = bl,y = bl, gäller ekvation 3.66:
3.66 \({I_{\rm{p}}} = \frac{{b_{\rm{l}}^4}}{6}\)
Om brädornas bredd inte är känd, kan bredden antas vara 80 mm.
Kontroll av knäckning hos väggar och pelare
Följande avsnitt i detta kapitel visar hur KL-trä används som väggskivor eller pelare och hur minsta erforderliga hållfasthet kan bestämmas enligt Eurokod 5. I likhet med de andra Eurokoderna, dimensioneras pelare i Eurokod 5 med hjälp av linjär knäckningsteori. De icke-linjära effekterna eller andra ordningens teori beaktas vid dimensioneringen med hjälp av en hållfasthetsrelaterad reduktionsfaktor kc. Vid kontroll av knäckning hos väggskivor och pelare av KL-trä är det i princip två olika laster som kan förekomma, rent axiellt tryck och transversallaster, se figur 3.27. Kombineras dessa laster ska uttryck enligt ekvationerna 3.67 och 3.68 uppfyllas:
3.67 \(\frac{{{\sigma _{{\rm{c}},{\rm{x}},{\rm{d}}}}}}{{{k_{\rm c,y}} \cdot \;{f_{{\rm{c}},0,{\rm{xlay}},{\rm{d}}}}}} + \frac{{{\sigma _{{\rm{m}},{\rm{y}},{\rm{d}}}}}}{{\;{f_{{\rm{m}},{\rm{xlay}},{\rm{d}}}}}} \le 1\)
3.68 \(\frac{{{N_{\rm{d}}}}}{{{k_{\rm c,y}} \cdot {A_{{\rm{x}},{\rm{net\;}}}} \cdot \;{f_{{\rm{c}},0,{\rm{xlay}},{\rm{d}}}}}} + \frac{{{M_{{\rm{y}},{\rm{d}}}}}}{{{W_{{\rm{x}},{\rm{net\;}}}} \cdot \;{f_{{\rm{m}},{\rm{xlay}},{\rm{d}}}}}} \le 1\)
med:
\({M_{{\rm{y}},{\rm{d}}}} = \frac{{{q_{\rm{d}}} \cdot l_e^2}}{8}\)
där uttrycket för reduktionsfaktorn kc,y kan skrivas enligt ekvation 3.69:
3.69 \({k_{\rm c,y}} = \frac{1}{{{k_\rm y} + \sqrt {k_{\mathop{\rm y}\nolimits} ^2 - \lambda _{\rm rel,y}^2} }} \le 1\)
där:
3.70 \({k_\rm y} = 0,5\left( {1 + 0,1\left( {{\lambda _{{\mathop{\rm rel}\nolimits} ,\rm y}} - 0,3} \right) + \lambda _\rm {rel,y}^2} \right)\)
\({\lambda _{{\mathop{\rm rel}\nolimits} ,\rm y}} = \frac{{{\lambda _{\mathop{\rm y}\nolimits} }}}{\pi }\sqrt {\frac{{\;{f_{{\rm{c}},0,{\rm{xlay}},{\rm{k}}}}}}{{{E_{\rm 0,x,05}}}}} \)
är relativ slankhetsfaktor för knäckning kring y-axeln.
\({\lambda _\rm y} = \frac{L}{{{i_\rm {x,ef}}}}\)
är slankhetsfaktorn och där ix,ef är slankhetsradien (se även avsnitt 3.3.4) och L är knäcklängden, med L = βc ∙ le och där βc antar värdet 0,1.
\({E_\rm {0,x,05}} = k \cdot {E_\rm {0,x,mean}}\)
med:
\(k = 1 - \frac{{0,328}}{{\sqrt {\frac{{2 \cdot {b_\rm x}}}{{0,15}} - 1} }}\)
med bx i meter och enligt figur 3.27.
I de fall λrel,y < 0,3 är risken för knäckning nästan obefintlig och då behöver man verifiera följande samband:
3.71 \({\left( {\frac{{{\sigma _{{\rm{c}},{\rm{x}},{\rm{d}}}}}}{{\;{f_{{\rm{c}},0,{\rm{xlay}},{\rm{d}}}}}}} \right)^2} + \frac{{{\sigma _{{\rm{m}},{\rm{y}},{\rm{d}}}}}}{{\;{f_{{\rm{m}},{\rm{xlay}},{\rm{d}}}}}} \le 1\)
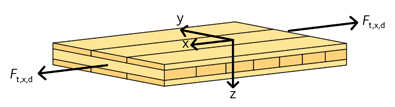
Figur 3.13 KL-träskiva med dragkraft parallellt med ytskiktet.
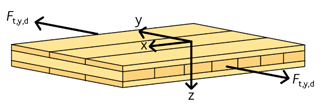
Figur 3.14 KL-träskiva med dragkraft vinkelrätt mot ytskiktet.
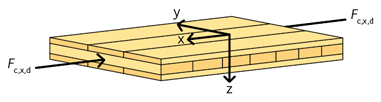
Figur 3.15 KL-träskiva med tryckkraft parallellt med ytskiktet.
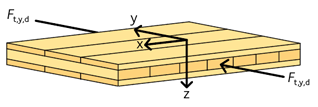
Figur 3.16 KL-träskiva med tryckkraft vinkelrätt mot ytskiktet.
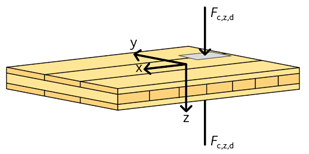
Figur 3.17 KL-träskiva med tryckkraft vinkelrätt mot sitt plan.
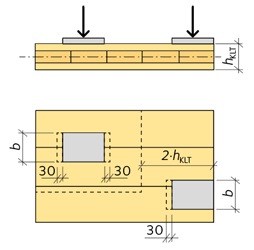
Figur 3.18 Effektiv kontaktyta för tryckkrafter vinkelrätt mot KL-träskivans plan. Värden för kant gäller inom avståndet 2 · hKLT från kanten.
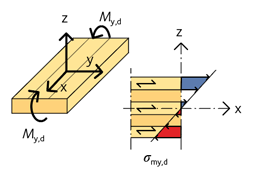
Figur 3.19 Böjspänningar i KL-träskiva med böjmoment kring y-axeln.
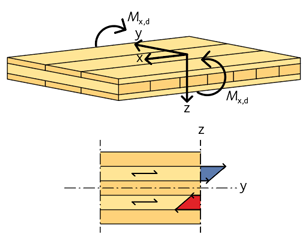
Figur 3.20 Böjspänningar i KL-träskiva med böjmoment kring x-axeln.
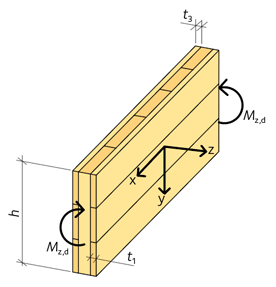
Figur 3.21 KL-träskiva med horisontella yttre brädskikt med böjmoment kring z-axeln.
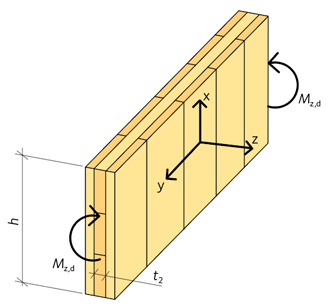
Figur 3.22 KL-träskiva med vertikala yttre brädskikt med böjmoment kring z-axeln.
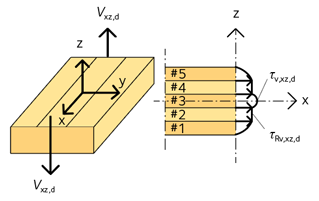
Figur 3.23 Skjuvspänningar av tvärkraft Vxz,d i KL-träskiva.
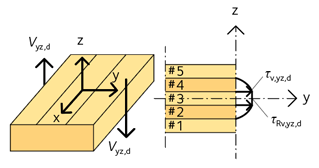
Figur 3.24 Skjuvspänningar av tvärkraft Vyz,d i KL-träskiva.
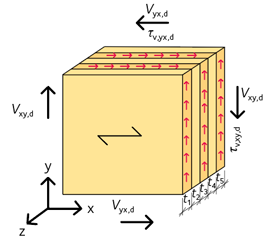
Figur 3.25 Skjuvspänningar i förhållande till skikttjocklek i KL-träskiva.
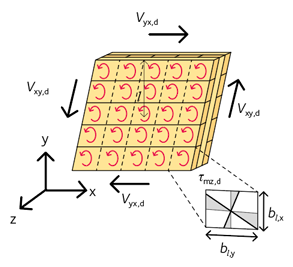
Figur 3.26 Skjuvspänningar mellan skikt i KL-träskiva.
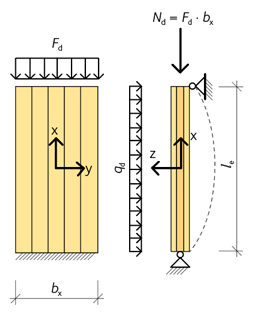
Figur 3.27 Väggskiva av KL-trä utsatt för transversallast samt tryckkraft och risk för knäckning.
Tabell 3.16 Kontaktyta A i mm2 och b i mm samt värde på kc,90.
| Läge | Riktning | Kontaktyta, Aef | kc,90 |
| Centralt | – | Aef = Atryck + (30 + 30)b | 1,9 |
| Vid kant | Parallellt med fibrerna | Aef = Atryck + (30 + 30)b | 1,0 – 1,5 |
| Vinkelrätt mot fibrerna | Aef = Atryck + 30b | 1,5 | |
| Vid hörn | – | Aef = Atryck + 30b | 1,3 |

