Nedan återges en översiktlig metod för att beräkna tvärsnittsstorheter, se ekvationerna 3.28 – 3.31 för osymmetriska tvärsnitt.
Bestämning av tyngdpunkten för tvärsnittet görs enligt följande:
- Ett referensskikt bestäms med Eref som elasticitetsmodul.
- Beräkna tyngdpunkten för varje skikt från tvärsnittets underkant, o1, o2, o3, …oi.
- Beräkna z-koordinaten från tvärsnittets underkant:
-
3.28 \({z_{\rm{s}}} = \frac{{\mathop \sum \nolimits^ \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}}b \cdot {t_{\rm{i}}}{o_{\rm{i}}}{\rm{\;}}}}{{\mathop \sum \nolimits^ \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}}b \cdot {t_{\rm{i}}}}}\)
- Nu kan avstånden ai mellan centrum av varje skikt och KL-träskivans neutrallager fastställas:
-
\({\rm a_{\rm{i}}} = \left| {{o_{\rm{i}}} - \;{z_{\rm{s}}}} \right|\)
Beräkning av nettoarea, med bärriktning i x-led:
3.29 \({A_{{\rm{x}},{\rm{net}}}} = \mathop \sum \nolimits^ \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}}{b_{\mathop{\rm x}\nolimits} }{t_{\rm{i}}}\)
Beräkning av tröghetsmoment, netto, med bärriktning i x-led:
3.30 \({I_{{\rm{x}},{\rm{net}}}} = \mathop \sum \nolimits^ \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}} \cdot \frac{{{b_\rm x}t_{\rm{i}}^3}}{{12}} + \mathop \sum \nolimits^ \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}}{b_\rm x}{t_{\rm{i}}}{a_{\rm{i}}}^2\)
Beräkning av böjmotstånd, netto, med bärriktning i x-led:
3.31 \({W_{{\rm{x}},{\rm{net}}}} = \frac{{{I_{{\rm{x}},{\rm{net}}}}}}{{{\rm{max}}\left\{ {\left| {{z_{\rm{ö}}}} \right|;\left| {{z_{\rm{u}}}} \right|} \right\}}}\)
Med zu = zs och zö = h |zs|
Vid bestämning av spänning under böjmoment My,d kan följande användas:
\({\sigma _{{\rm{m}},\rm y,{\rm{d}}}} = \frac{{{E_{\rm{i}}}}}{{{E_{{\rm{ref}}}}}} \cdot \frac{{{M_{{\rm{y}},{\rm{d}}}}}}{{{W_{{\rm{x}},{\rm{net}}}}}}\)
där:
| Ei | är det enskilda skiktets elasticitetsmodul. |
| Eref | är valt referensvärde för elasticitetsmodul. |
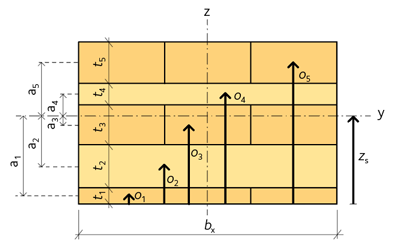
Figur 3.8 Uppbyggnad och numrering av ett osymmetriskt tvärsnitt.

