Materialvärden: E0 = 11 000 MPa för virke i hållfasthetsklass C24, E90 = 0 MPa, G090 = 650 MPa och G9090 = 50 MPa.
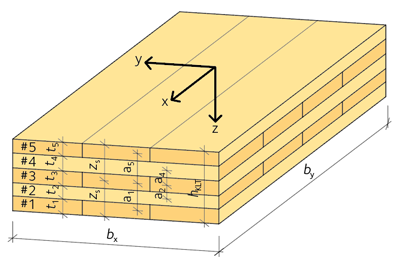
Figur 3.31 Definition av riktningar och mått.
Tabell 3.17 Uppbyggnad av 5-skikts symmetrisk KL-träplatta.
| Skikt | Riktning | Tjocklek (mm) | Hållfasthetsklass |
| 5 | Längs, x-riktning | 20 | C24 |
| 4 | Tvärs, y-riktning | 40 | C24 |
| 3 | Längs, x-riktning | 20 | C24 |
| 2 | Tvärs, y-riktning | 40 | C24 |
| 1 | Längs, x-riktning | 20 | C24 |
Tabell 3.18 Egenskaper för 5-skikts symmetrisk KL-träplatta enligt ovan.
| Egenskap | Beräkningsformel |
| Tyngdpunktscentrum (mm) |
\({z_\rm s} = \frac{{{h_{{\mathop{\rm KLT}\nolimits} }}\;}}{2}\) |
| Nettotröghetsmoment (mm4) |
\({I_{{\rm{x}},{\rm{net}}}} = {b_{\rm{x}}}\left( {\frac{{t_1^3}}{{12}} + {t_1}{a_1}^2 + \frac{{t_3^3}}{{12}} + {t_3}{a_3}^2 + \frac{{t_5^3}}{{12}} + {t_5}{a_5}^2} \right)\) \( = {b_{\rm{x}}}\left( {3 \cdot \frac{{t_1^3}}{{12}} + 2 \cdot {t_1}{a_1}^2} \right)\) |
| Nettoböjmotstånd (mm3) |
\({W_{{\mathop{\rm x}\nolimits} ,\rm net}} = \frac{{2 \cdot {I_{x,{\rm{net}}}}}}{{{h_{{\rm{KLT}}}}}}\) |
| Skjuvkapacitet i längdriktning (kN) |
\({S_{{\rm{x}},{\rm{KLT}}}} = {\kappa _x}{b_{\rm{x}}}\left( {{G_0}{t_1} + {G_{90}}{t_2} + {G_0}{t_3} + \ldots } \right)\) \( = {\kappa _x}{b_{\rm{x}}}\left( {3 \cdot {G_0}{t_1} + 2 \cdot {G_{90}}{t_2}} \right)\) |
| Nedböjning vid 5 kN centrisk punktlast vid fri spännvidd L = 6 m, enligt Timoshenko | \({w_{5{\rm{kN}}}} = \frac{{P{L^3}}}{{48 \cdot {E_0} \cdot {I_{{\rm{x}},{\rm{net}}}}}} + \frac{{P \cdot L}}{{4 \cdot {S_{{\rm{x}},{\rm{KLT}}}}}}\) |
| Nedböjning av 3 kN/m vid fri spännvidd L = 6 m, enligt Timoshenko | \({w_{3{\rm{kN}}/{\rm{m}}}} = \frac{{5 \cdot q{L^4}}}{{384 \cdot {E_0} \cdot {I_{{\rm{x}},{\rm{net}}}}}} + \frac{{q{L^2}}}{{8 \cdot {S_{{\rm{x}},{\rm{KLT}}}}}}\) |
| Effektivt tröghetsmoment (mm4) för fri spännvidd \(l\)ref = 6 m | \({\gamma _1} = {\gamma _5} = \frac{1}{{1 + \frac{{{\pi ^2}{E_{{\rm{x}},1}}{t_1}}}{{l_{{\rm{ref}}}^2}}\; \cdot \frac{{{t_2}}}{{{G_{9090,2}}}}}}\) \({I_{{\rm{x}},{\rm{ef}}}} = {b_\rm x}\left( {\frac{{3 \cdot t_1^3}}{{12}} + 2{\gamma _1}{t_1}{a_1}^2} \right)\) |
| Nedböjning vid 5 kN centrisk punktlast vid fri spännvidd L = 6 m, enligt Gammametod | \({w_\rm {5kN}} = \frac{{P{L^3}}}{{48 \cdot {E_0} \cdot {I_\rm {x,ef}}}}\) |
| Nedböjning av 3 kN/m vid fri spännvidd L = 6 m, enligt Gammametod | \({w_\rm {3kN/m}} = \frac{{5 \cdot q{L^4}}}{{384 \cdot {E_0} \cdot {I_{{\mathop{\rm x}\nolimits} ,\rm ef}}}}\) |
| Egenskap | Tillämpning för exemplet |
| Tyngdpunktscentrum (mm) |
\({z_\rm s} = \frac{{140\;}}{2} = 70\;{\rm{mm}}\) |
| Nettotröghetsmoment (mm4) |
\({I_{{\rm{x}},{\rm{net}}}} = 1000\left( {3 \cdot \frac{{{{20}^3}}}{{12}} + 2 \cdot 20 \cdot {{60}^2}} \right) = 14600 \cdot {10^4}{\rm{\;m}}{{\rm{m}}^4}\) |
| Nettoböjmotstånd (mm3) |
\({W_{{\mathop{\rm x}\nolimits} ,\rm net}} = \frac{{2 \cdot 14600 \cdot {{10}^4}}}{{140}} = 2086 \cdot {10^3}\;{\rm{m}}{{\rm{m}}^3}\) |
| Skjuvkapacitet i längdriktning (kN) |
\({\kappa _x} = 0,208\) enligt tabell 3.10 \({S_{{\rm{x}},{\rm{KLT}}}} = 0,208 \cdot 1000 \cdot \left( {3 \cdot 650 \cdot 20 + 2 \cdot 50 \cdot 40} \right) = 8944\;{\rm{kN}}\) |
| Nedböjning vid 5 kN centrisk punktlast vid fri spännvidd L = 6 m, enligt Timoshenko | \({w_{5{\rm{kN}}}} = \frac{{5 \cdot {{10}^3} \cdot {{6000}^3}}}{{48 \cdot 11000 \cdot 14600 \cdot {{10}^4}}} + \) \(\frac{{5 \cdot {{10}^3} \cdot 6000}}{{4 \cdot 8944 \cdot {{10}^3}\;}} = 14,0 + 0,8 = 14,8\;{\rm{mm}}\) |
| Nedböjning av 3 kN/m vid fri spännvidd L = 6 m, enligt Timoshenko | \({w_{3{\rm{kN}}/{\rm{m}}}} = \frac{{5 \cdot 3 \cdot {{6000}^4}}}{{384 \cdot 11000 \cdot 14600 \cdot {{10}^4}}} + \) \(\frac{{3 \cdot {{6000}^2}}}{{8 \cdot 8944 \cdot {{10}^3}\;}} = 31,5 + 1,5 = 33,0{\rm{\;mm}}\) |
| Effektivt tröghetsmoment (mm4) för fri spännvidd \(l\)ref = 6 m | \({\gamma _1} = {\gamma _5} = \frac{1}{{1 + \frac{{{\pi ^2} \cdot 11000 \cdot 20}}{{{{6000}^2}}} \cdot \frac{{40}}{{50}}}} = 0,9849\) \({I_{{\rm{x}},{\rm{ef}}}} = 1000\left( {\frac{{{{20}^3}}}{4} + 2 \cdot 0,9849 \cdot 20 \cdot {{65}^2}} \right) = 14382 \cdot {10^4}{\rm{\;m}}{{\rm{m}}^4}\) |
| Nedböjning vid 5 kN centrisk punktlast vid fri spännvidd L = 6 m, enligt Gammametod | \({w_\rm {5kN}} = \frac{{5 \cdot {{10}^3} \cdot {{6000}^3}}}{{48 \cdot 11000 \cdot 14382 \cdot {{10}^4}}} = 14,2{\rm{\;mm}}\) |
| Nedböjning av 3 kN/m vid fri spännvidd L = 6 m, enligt Gammametod | \({w_\rm {3kN/m}} = \frac{{5 \cdot 3 \cdot {{6000}^4}}}{{384 \cdot 11000 \cdot 15959 \cdot {{10}^4}}} = 32,0{\rm{\;mm}}\) |

